决策边界算法

决策边界 (decision boundary)

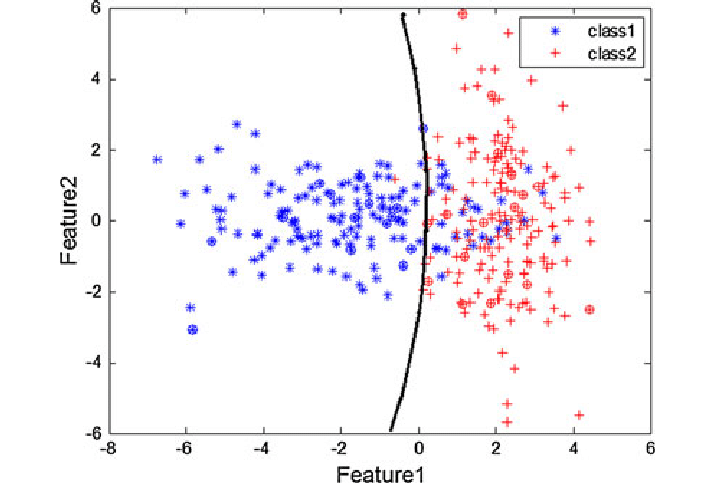
支持向量机获取这些数据点并输出最能分离标签的超平面。这条线是决策边界

决策平面 （ decision surface ），是将空间划分为不同的区域。位于决策平面一侧的数据被定义为与位于另一侧的数据属于不同的类别。决策面可以作为学习过程的结果创建或修改，它们经常用于机器学习、模式识别和分类系统。

环境空间 ( Ambient Space)，围绕数学对象即对象本身的空间，如一维 Line ，可以独立研究，这种情况下L则是L；再例如将L作为二维空间 $R^2$ 的对象进行研究，这种情况下 L 的环境空间是 $R^2$。

超平面（Hyperplane）是一个子空间， N维空间的超平面是其具有维数的平面的子集。就其性质而言，它将空间分成两个半空间，其维度比其环境空间的维度小 1。如果空间是三维的，那么它的超平面就是二维维平面，而如果空间是 2 维的，那么它的超平面就是一维线。支持向量机 (SVM) 通过找到使两个类之间的边距最大化的超平面来执行分类。

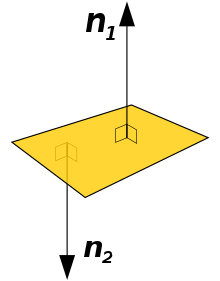
法向量 （Normal） 是垂直于该平面、另一个向量的 90° 角倾斜

什么是支持向量

支持向量 （Support vectors），靠近决策平面（超平面）的数据点。

如图所示，从一维平面来看，哪个是分离的超平面？

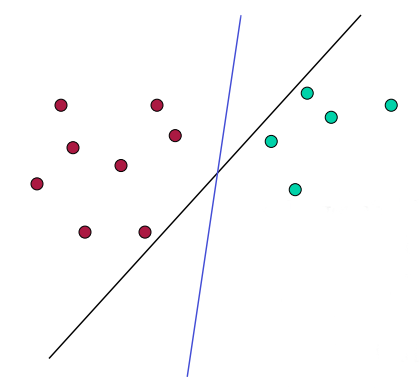
一般而言，会有很多种解决方法（超平面），支持向量机就是如何找到最佳方法的解决方案。

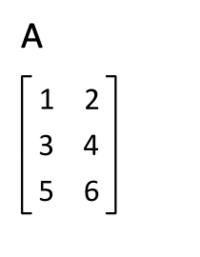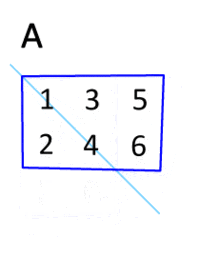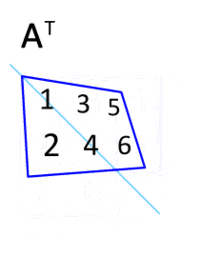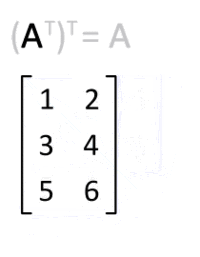
转置运算

矩阵的转置是原始矩阵的翻转版本，可以通过转换矩阵的行和列来转置矩阵。我们用 $A^T$ 表示矩阵 A 的转置。例如，$$A=\left[ \begin{matrix} 1 & 2 & 3 \ 4 & 5 & 6 \ \end{matrix} \right]$$ ；那么 A 的转置就为 $$A=\left[ \begin{matrix} 1 & 4 \ 2 & 5 \ 3 & 6 \ \end{matrix} \right]$$ ；

我们可以将向量的转置作为特例。由于 n 维向量 x 由 n×1 列矩阵表示：$$x=\left[ \begin{matrix} x_1 \ x_2 \ x_3 \ …. \ x_n \ \end{matrix} \right]$$ ；那么 x 的转置（$x^T$）是一个 $1\times n$ 行矩阵 $$x^T=\left[ \begin{matrix} x_1 & x_2 & x_3 & … & x_n \ \end{matrix} \right]$$ 。

权重向量

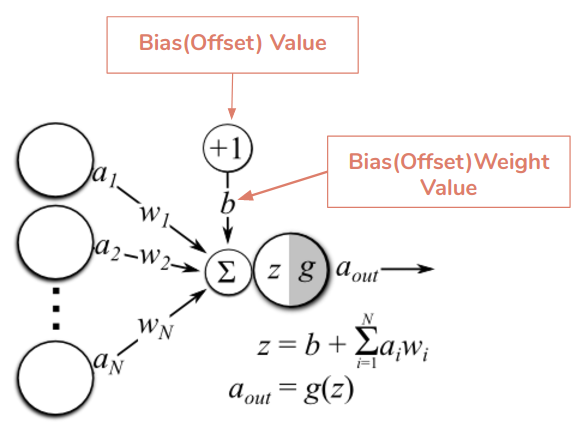
$wx+b=0$ w：权重向量 x n维向量 $x_i=[1,2,3…n]$ $w_i=[1,2,3…n]$ 每个输入的值都乘以一个“权重” $w_i$。权重是表示计算输出时每个输入的重要性的值

权重决定了输入对输出的影响程度。 $Y=\sum(Weight \times input)+bias$ ；如果输入为 $[x_1,x_2\ … ,x_n]$ 权重是：$[w_1,w_2\ \ ,w_n]$

通过场景来理解

假设预估汽车的价格，汽车的价格取决于制造年份和行驶里程数。让我们假设汽车的年份越高，汽车价格越高。随后，汽车开得越多，汽车就越便宜。

这个例子应该可以帮助您了解汽车价格与制造年份之间存在正相关关系，而汽车价格与其行驶里程之间存在负关关系。因此，我们希望看到代表年份的特征的权重为正，代表里程的特征的权重为负。公式为：$car = (w_1x\ ear+w_2x\ miles)$

偏差 bais 是一个常数 const ，偏差用于将影响函数的结果向正或负方向移动。bias 会被被添加到 input 和 weight 的乘积中。偏差用于抵消结果。$x_1w_1+x_2w_2…x_nw_n+bias$

通过场景来理解

假设希望在输入为 0 时返回 2。由于权重和输入的乘积之和为 0，您将如何确保返回 2？此时可以添加2的bias。如果不包含偏差，只是对 input 和 weight 执行矩阵乘法。这将很容易导致过度拟合数据集。

过度拟合（overfitting）是指机器学习算模型在训练集上的误差和测试集上的误差之间差异过大。造成过度拟合的原因可能有多种．最常见的就是模型容量过高，模型过于复杂，换句话说是模型假设所包含的参数数量过多．如此一来，算法会将训练集中所包含的没有普遍性的一些特征也学习进来，结果降低了模型的泛化能力．

https://machine-learning.paperspace.com/wiki/weights-and-biases

范数

向量的范数（norm）是它的长度 ，x的范数表示为 $\parallel x \parallel$；常用的范数为 P 范数，其中 P 是大于等于1的任何数，向量 x的 p 范数表示为 $\parallel x \parallel_p$ ；通常情况下向量 x 的 p 范数的计算公式为： $\parallel x \parallel_p = (x_1^p+x_2^p+x_3^p+ \ …\ x_n^p)^{1/p}$ ；公式可以简写为：$\parallel x \parallel_p = (\sum_{i=1}^n\ x_i^p)^{1/p}$

曼哈顿距离

曼哈顿距离也被称为1-范数 1-norm，因为它测量的中两点之间的距离。假设：向量a，我们必须计算 1-范式 $\vec{a} = [2,3]$ ，在图像中表示（红色线部分表示向量a的1-范式）

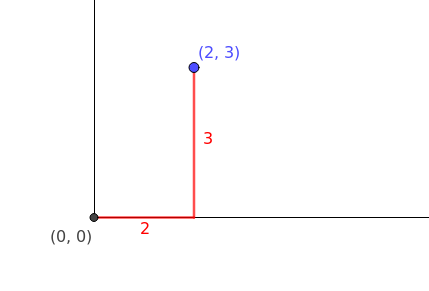
通过公式来计算1-范式，可以将p替换为1，$\parallel a \parallel_1 = (x_1 + x_2) = (2+3)^1=5$

欧几里得范数

欧几里得范数又被称作2-范数 2-norm ，是范数中最常用的范数，欧几里得范数返回的是两点之间最短的距离，因此 $\vec{a}$ 的2-范式为 $\parallel x \parallel_2 = (2^2+3^2)^{\frac{1}{2}} = (4+9)^{\frac{1}{2}} = \sqrt{13}$ ；用图像表示为（红线部分表示2-范数，这是 $\vec{a}$ 表示的点到点之间的最低按距离）

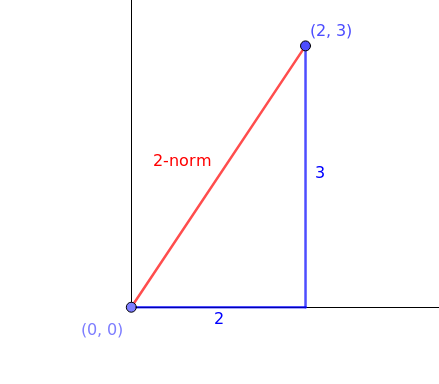
无穷范数

无穷范数 Infinity-norm 是返回给定向量中的最大绝对值；$\vec{a}$ 的无穷范式为 $\parallel a \parallel_\infty = 3$ （公式求得是上述图中 $[2,3]$ 这个实例）。

例如，如果我们必须找到一个向量的无穷范数，比如 $\vec{b}$ ，$\vec{b} = [4,3,-1]$ ；那么 $\parallel b \parallel_\infty = 6$ （这里最大是4，但是返回的是一个绝对值所以是6）

Reference

norm

vector norms

拉格朗日乘子法

拉格朗日乘子法 Lagrange multiplier，是一种寻找受等式约束的函数的局部最大值和最小值的策略（即，必须满足一个或多个方程必须完全满足所选变量值的条件）

设置超平面为 $wx+b=0$ ，其中 $w=[1,2,\ ..,\ n]$ ，w是 $n \times 1$ 维，n特征值的个数，x 训练的示例，b是bias，一个二维的超平面的特征为：$x=[x_1,x_2]$ ，$w=[w_1,w_2]$ ，b看做 wegiht $w_0$ ，

那么这个超平面的方程就为：$$ f(n) \begin{cases} w_1x_1+w_2x_2+w0 = 0\ \ 超平面(决策边界)方程 \ w_1x_1+w_2x_2+w0 > 0\ \ 超平面(决策边界)上部分 \ w_1x_1+w_2x_2+w0 < 0\ \ 超平面(决策边界)下部分 \ \end{cases} $$ ，那么在对公式进行分解，增加参数 y ，代表了对向量的分类，也就是说超平面两边的向量，这样公式为：$$ f(n) \begin{cases} w_1x_1+w_2x_2+w0 \ge 1\ \ 当 y_i = +1 \ w_1x_1+w_2x_2+w0 \le 1\ \ 当 y_i = -1 \ \end{cases} $$